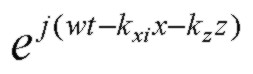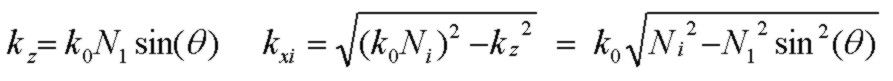Reflectivity Roots

Oct 28, 2014
This article discusses plane wave multi-layer reflectivity problems and square-root sign selection. The geometry used and exponential sign convention is shown below. The plane of incidence is the XZ plane. In steady state, continuity of all tangential E and H vector field components at all interfaces implies a common temporal and Z exponential dependence shown below with the same kz value in each layer (general Snell's law). Each medium will have a different normal component of complex propogation constant kxi. All media, including the incident medium N1 may have loss implying that kz and all kxi values may be complex:







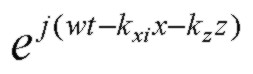
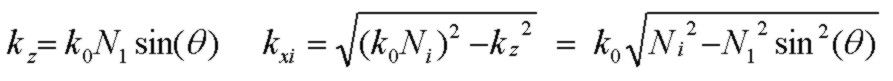
where media with loss, using the above exponential sign convention, are described by a complex refractive index with NEGATIVE imaginary part, e.g. N = 3.2 - j0.05.

Case 1: Incident Medium REAL (no loss)

In this case with REAL kx1 and kz, a uniform non-attenuating plane wave is incident at some real angle θ. With the exponential sign convention above, the correct square root sign selection for kxi must have a NEGATIVE imaginary part, for media with loss, to describe attenuation in the +x propogation direction downward and normal to the layer interfaces. There is no ambiguity in this case.

Case 2: Incident Medium COMPLEX (lossy)

In this unusual and somewhat unintiutive case, an attenuating homogeneous plane wave (planes of equal phase and amplitude are parallel) is incident at some REAL angle θ. kz is now complex, but again must be the same in each medium. In this case, depending on the angle of incidence and the loss in the other layers, the kxi values may have real and imaginary parts that are negative OR positive. This is a consequence of the field attenuation in the incident medium which means that the higher field values at smaller values of Z to the left will refract into correspondingly higher values of field compared to values refracted at higher Z values to the right. If the medium refracted into has low or no loss, an exponential GROWTH of field normal to the layers in the final medium is possible. Furthermore, in situations with TIR, phase fronts of the refracted field (including in the final medium) may be directed INWARD to the final interface. In cases with a lossy incident medium, it appears that special cases must be examined to determine physical validity, depending on the root selected for kxi. Also it must remembered that any infinite plane wave is an idealization. This is particularly obvious when discussing incident media with loss: an infinite plane wave has infinitely increasing amplitude back towards its source!


Reference: